Линко
Новая платформаЛинко
Скрыть менюГлавная
Поиск. Обзор сервисов Назад в раздел
Статьи по данной теме


Примеры расчетов неопределенности и постановки эксперимента. Отбор пробы часто вносит существенный вклад в неопределенность и требует тщательного планирования и контроля. В связи с этим ужесточаются требования по оценке неопределенности, связанной с процессом отбора пробы. Какие НД требуют оценивать неопределенность отбора пробы? ГОСТ ISO/IEC 17025-2019 прямо говорит о том, что “лаборатории должны определять вклад(ы) в неопределенность измерений“ и “при оценивании неопределенности измерений все существенные вклады, в том числе связанные с отбором образцов, должны учитываться с применением соответствующих методов анализа (п. 7.6.1).
Вступление
Какие НД требуют оценивать неопределенность отбора пробы?
Какие бывают неопределенности?
Подходы к оценке неопределенности
Экспериментальный подход
Пример оценки неопределенности измерений с использованием экспериментального подхода
Теоретический подход
Контроль качества результатов измерений с учетом неопределенности отбора проб
Что вносит наибольший вклад в неопределенность отбора проб?
Неопределенность измерения – наиболее важный обобщенный параметр, характеризующий качество измерений. В настоящее время в разработке методов оценки неопределенности, возникающей на аналитическом этапе измерения, достигнут значительный прогресс, однако измерение почти всегда включает процесс отбора пробы.
Отбор пробы часто вносит существенный вклад в неопределенность и требует тщательного планирования и контроля. В связи с этим ужесточаются требования по оценке неопределенности, связанной с процессом отбора пробы.
ГОСТ ISO/IEC 17025-2019 прямо говорит о том, что “лаборатории должны определять вклад(ы) в неопределенность измерений“ и “при оценивании неопределенности измерений все существенные вклады, в том числе связанные с отбором образцов, должны учитываться с применением соответствующих методов анализа (п. 7.6.1).
Также Примечание 1 к п. 7.6.3 позволяет считать оценку неопределенности выполненной, “если хорошо известный метод испытаний устанавливает пределы значений основных источников неопределенности измерений и указывает форму представления результатов”, а лаборатория следует методу испытаний и инструкции по представлению результатов. Однако, лаборатория должна уметь показать, что “выявленные критические факторы, оказывающие влияние, находятся под контролем”, а значит контролировать качество результатов измерений и демонстрировать постоянство составляющих неопределенности, в том числе неопределенности отбора проб.
Существуют различные источники неопределенности, и их классифицируют различными способами. Руководство Eurachem по оценке неопределенности говорит о восьми основных категориях, куда относятся такие факторы как неоднородность объекта, транспортирование и хранение проб, загрязнение, пробоподготовка, погрешности разбавления и т.д. В самом простом виде классификацию источников неопределенности можно свести к двум категориям: "неопределенность отбора пробы" и "неопределенность анализа".
Существуют два основных подхода к оценке неопределенности. Согласно одному из них, называемому "экспериментальным", "эмпирическим", "ретроспективным" или "нисходящим", выполняют определенное количество повторов полной процедуры измерения, чтобы получить прямую оценку неопределенности для окончательного результата измерения.
Второй подход, который называют "теоретическим", "модельным", "расчетным" или "восходящим", состоит в количественной оценке каждого отдельного источника неопределенности и последующем их объединении с использованием некоторой принятой модели.
Эти подходы взаимно не исключают друг друга. Каждый из них имеет свои преимущества в определенных обстоятельствах.
Целью экспериментального подхода является достоверное оценивание неопределенности без обязательного знания каких-либо отдельных ее составляющих. В рамках этого подхода можно описать общий вид источников неопределенности и подразделить их на те, которые возникают в процессе отбора пробы и во время анализа. А рассчитав количественные оценки для каждого из факторов по отдельности и объединив их, получить оценку неопределенности результата измерения в целом.
Экспериментальный подход можно относительно быстро и легко применить на практике (особенно для "метода двойных проб"). Его методы являются в целом более применимыми для самых различных материалов и не зависят так сильно от наличия предварительной информации о системе или всех источниках неопределенности. В связи с этим их реализация требует меньше времени и, следовательно, затрат, что особенно важно при разовых исследованиях различных целевых объектов.
Модель случайных эффектов от одного объекта пробоотбора описывается следующей формулой:
X = Xtrue + εsample + εanalysis ,
где Xtrue — истинное (действительное) значение измеряемой величины; εsample — составляющая неопределенности, обусловленная процедурой пробоотбора; εanalysis — составляющая неопределенности, обусловленная процедурой анализа.
Для единичного целевого объекта, если источники дисперсии независимы, дисперсия результата измерения σ2meas описывается уравнением:
σ2meas = σ2sample + σ2analysis ,
а аппроксимация значений дисперсий их статистическими оценками дает выражение:
s2meas = s2sample + s2analysis
В этом случае cтандартную неопределенность измерений с учетом вклада дисперсии пробоотбора рассчитывают по формуле:
u = smeas = (s2sample + s2analysis)0,5
(1) ❯
Дисперсию, обусловленную физической подготовкой пробы, можно включить в дисперсию отбора пробы или, при необходимости, выразить ее отдельным членом уравнения (s2prep).
При исследовании на нескольких целевых объектах, которое рекомендуется проводить для оценивания неопределенности отбора пробы, модель нужно расширить:
X = Xtrue + εtarget + εsample + εanalysis ,
где дополнительный член εtarget характеризует рассеяние концентрации между целевыми объектами.
Оценки дисперсий s2target, s2sample и s2analysis могут быть получены по методике «анализ дисперсии» (ANOVA), детальное описание которой дано, например, в ГОСТ Р ИСО 5725-3 (см. приложение В.1). При этом оценками s2target, s2sample и s2analysis являются s2(0), s2(1) и s2r соответственно.
Отбор можно осуществлять по схеме, приведенной на рисунке 1.
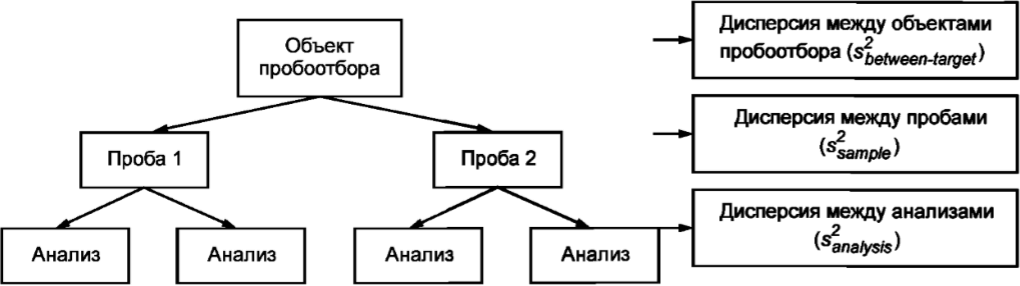
Рисунок 1. План пробоотбора
Схема описывает отбор по методу двойных проб. Он заключается в том, что один пробоотборщик дублирует часть проб (например, 10 %, но не менее чем от восьми объектов пробоотбора). Если есть только один объект, то все восемь двойных проб можно отбирать из него, но тогда оценка неопределенности будет применима только к этому объекту. Пробоотборщик отбирает параллельные пробы. Затем обе параллельные пробы подвергают пробоподготовке, в результате чего получают две отдельные лабораторные пробы. Каждую пробу анализируют независимо в условиях повторяемости.
Прежде всего уточним формулу расчета суммарной cтандартной неопределенности измерений (u). В большинстве случаев лаборатория работает с аттестованными методиками измерений, в которых суммарная стандартная неопределенность анализа уже рассчитана и приведена. Поэтому уравнение (1) будет иметь вид:
u = (s2sample + u2analysis)0,5
(2) ❯
а для исследования на нескольких целевых объектах:
u = (s2target + s2sample + u2analysis)0,5
(3) ❯
где u – суммарная cтандартная неопределенность измерений,
s
2sample – дисперсия между пробами,
s
2target – дисперсия между объектами пробоотбора
u
analysis - суммарная стандартная неопределенность анализа, приведенная в методике.
Расширенную неопределенность измерений U рассчитывают по формуле:
U = k × u
(4) ❯
где k — коэффициент охвата (k = 2 при Р = 0,95).
Рассмотрим пример оценки неопределенности измерений концентрации некоторого компонента, содержащегося в материале, пробы которого отбираются с 8 объектов по методу двойных проб (рисунок 1). Результаты измерения концентрации анализируемого компонента приведены в таблице 1.
Таблица 1. Результаты измерения концентрации анализируемого компонента
|
Номер объекта пробоотбора |
Номер пробы | Результат измерений, мг/дм³ | |
| yij1 | yij2 | ||
| 1 | 1 | 2,65 | 2,43 |
| 2 | 2,52 | 2,45 | |
| 2 | 1 | 1,98 | 2,10 |
| 2 | 2,03 | 2,14 | |
| 3 | 1 | 2,41 | 2,58 |
| 2 | 2,29 | 2,37 | |
| 4 | 1 | 3,16 | 3,01 |
| 2 | 3,05 | 3,19 | |
| 5 | 1 | 2,72 | 2,80 |
| 2 | 2,86 | 2,93 | |
| 6 | 1 | 2,32 | 2,46 |
| 2 | 2,29 | 2,41 | |
| 7 | 1 | 1,76 | 1,89 |
| 2 | 1,84 | 1,86 | |
| 8 | 1 | 2,43 | 2,52 |
| 2 | 2,56 | 2,68 | |
Используя алгоритмы, приведенные в ГОСТ Р ИСО 5725-3 (приложение В.1), рассчитаем:
Таблица 2. Расчет дисперсии между анализами (s2analysis)
|
Номер объекта пробоотбора |
Номер пробы |
Результат измерений, мг/дм³ |
wij(1), wij(1) = |yij1 - yij2| |
wij(1)2 |
SSe, SSe = (Σ wij(1)2) / 2 |
MSe, MSe = SSe / 2p |
sr2*, sr2 = MSe |
|
| yij1 | yij2 | |||||||
| 1 | 1 | 2,65 | 2,43 | 0,22 | 0,04840 | 0,12115 | 0,00757 | 0,00757 |
| 2 | 2,52 | 2,45 | 0,07 | 0,00490 | ||||
| 2 | 1 | 1,98 | 2,10 | 0,12 | 0,01440 | |||
| 2 | 2,03 | 2,14 | 0,11 | 0,01210 | ||||
| 3 | 1 | 2,41 | 2,58 | 0,17 | 0,02890 | |||
| 2 | 2,29 | 2,37 | 0,08 | 0,00640 | ||||
| 4 | 1 | 3,16 | 3,01 | 0,15 | 0,02250 | |||
| 2 | 3,05 | 3,19 | 0,14 | 0,01960 | ||||
| 5 | 1 | 2,72 | 2,80 | 0,08 | 0,00640 | |||
| 2 | 2,86 | 2,93 | 0,07 | 0,00490 | ||||
| 6 | 1 | 2,32 | 2,46 | 0,14 | 0,01960 | |||
| 2 | 2,29 | 2,41 | 0,12 | 0,01440 | ||||
| 7 | 1 | 1,76 | 1,89 | 0,13 | 0,01690 | |||
| 2 | 1,84 | 1,86 | 0,02 | 0,00040 | ||||
| 8 | 1 | 2,43 | 2,52 | 0,09 | 0,00810 | |||
| 2 | 2,56 | 2,68 | 0,12 | 0,01440 | ||||
* в ГОСТ Р ИСО 5725-3 s2analysis обозначена как sr2; p = 8 (количество объектов пробоотбора)
Таблица 3. Расчет дисперсии между пробами (s2sample)
|
Номер объекта пробоотбора |
Номер пробы |
Результат измерений, мг/дм³ |
yi1 ср, yi1 ср = (yij1 + yij2) / 2 (проба №1) |
wi(2), wi(2) = |yi1 ср - yi2 ср| |
wi(2)2 |
SS1, SS1 = Σ wi(2)2 |
MS1, MS1 = SS1 / p |
s(1)2**, s(1)2 = (MS1 - MSe) / 2 |
|
| yij1 | yij2 |
yi2 ср, yi2 ср = (yij1 + yij2) / 2 (проба №2) |
|||||||
| 1 | 1 | 2,65 | 2,43 | 2,54 | 0,05 | 0,00302 | 0,07498 | 0,00937 | 0,00090 |
| 2 | 2,52 | 2,45 | 2,49 | ||||||
| 2 | 1 | 1,98 | 2,10 | 2,04 | 0,04 | 0,00202 | |||
| 2 | 2,03 | 2,14 | 2,09 | ||||||
| 3 | 1 | 2,41 | 2,58 | 2,50 | 0,17 | 0,02723 | |||
| 2 | 2,29 | 2,37 | 2,33 | ||||||
| 4 | 1 | 3,16 | 3,01 | 3,09 | 0,04 | 0,00123 | |||
| 2 | 3,05 | 3,19 | 3,12 | ||||||
| 5 | 1 | 2,72 | 2,80 | 2,76 | 0,14 | 0,01823 | |||
| 2 | 2,86 | 2,93 | 2,90 | ||||||
| 6 | 1 | 2,32 | 2,46 | 2,39 | 0,04 | 0,00160 | |||
| 2 | 2,29 | 2,41 | 2,35 | ||||||
| 7 | 1 | 1,76 | 1,89 | 1,83 | 0,03 | 0,00063 | |||
| 2 | 1,84 | 1,86 | 1,85 | ||||||
| 8 | 1 | 2,43 | 2,52 | 2,48 | 0,15 | 0,02103 | |||
| 2 | 2,56 | 2,68 | 2,62 | ||||||
** в ГОСТ Р ИСО 5725-3 s2sample обозначена как s(1)2; p = 8 (количество объектов пробоотбора)
Таблица 4. Расчет дисперсии между объектами пробоотбора (s2target)
|
Номер объекта пробоотбора |
Номер пробы |
Результат измерений, мг/дм³ |
yi1 ср, yi1 ср = (yij1 + yij2) / 2 (проба №1) |
yi ср, yi ср = (yi1 ср + yi2 ср) / 2 |
yi ср2 |
yобщ ср, yобщ ср = Σ yi ср / p |
SS0, SS0 = 4Σ (yi ср)2 - 4p (yобщ ср)2 |
MS0, MS0 = SS0 / (p - 1) |
s(0)2***, s(0)2 = (MS0 - MS1) / 4 |
|
| yij1 | yij2 |
yi2 ср, yi2 ср = (yij1 + yij2) / 2 (проба №2) |
||||||||
| 1 | 1 | 2,65 | 2,43 | 2,54 | 2,51 | 6,31266 | 2,46 | 4,45655 | 0,63665 | 0,15682 |
| 2 | 2,52 | 2,45 | 2,49 | |||||||
| 2 | 1 | 1,98 | 2,10 | 2,04 | 2,06 | 4,25391 | ||||
| 2 | 2,03 | 2,14 | 2,09 | |||||||
| 3 | 1 | 2,41 | 2,58 | 2,50 | 2,41 | 5,82016 | ||||
| 2 | 2,29 | 2,37 | 2,33 | |||||||
| 4 | 1 | 3,16 | 3,01 | 3,09 | 3,10 | 9,62551 | ||||
| 2 | 3,05 | 3,19 | 3,12 | |||||||
| 5 | 1 | 2,72 | 2,80 | 2,76 | 2,83 | 7,99476 | ||||
| 2 | 2,86 | 2,93 | 2,90 | |||||||
| 6 | 1 | 2,32 | 2,46 | 2,39 | 2,37 | 5,61690 | ||||
| 2 | 2,29 | 2,41 | 2,35 | |||||||
| 7 | 1 | 1,76 | 1,89 | 1,83 | 1,84 | 3,37641 | ||||
| 2 | 1,84 | 1,86 | 1,85 | |||||||
| 8 | 1 | 2,43 | 2,52 | 2,48 | 2,55 | 6,48976 | ||||
| 2 | 2,56 | 2,68 | 2,62 | |||||||
*** в ГОСТ Р ИСО 5725-3 s2target обозначена как s(0)2; p = 8 (количество объектов пробоотбора)
Полученные дисперсии между пробами и между объектами пробоотбора соответствуют неопределенностям, возникающим при отборе проб с одного и с нескольких объектов.
Поскольку в используемой методике приведено относительное значение uanalysis (7,5%), будет удобно представить дисперсию между пробами также в виде относительной неопределенности:
usample отн = ((s2sample)0,5 × 100) / yобщ ср
usample отн = (0,00090,5 × 100) / 2,46
usample отн = 1,22 %
Подставив найденное значение неопределенности отбора проб в уравнение (2) получим:
u = (1,222 + 7,52)0,5
u = 7,6 %
Расширенная относительная неопределенность согласно уравнению (4) будет равна 15,2%, что в данном примере говорит об увеличении суммарной неопределенности измерений на 0,2% при учете неопределенности, вносимой отбором проб.
Аналогично, используя дисперсию между объектами пробоотбора, из уравнения (3) можно найти суммарную неопределенность измерений с учетом отбора проб на разных объектах.
Дисперсия между анализами (s2analysis) не только необходима для расчета остальных дисперсий, но и может быть использована для расчета собственной лабораторной неопределенности анализа при условии, что она не превышает значение неопределенности, установленное методикой, и обеспечено контролем стабильности результатов измерений.
Сущность подхода состоит в том, что вначале выявляют все источники неопределенности, количественно оценивают вклад каждого источника, а затем сводят все составляющие в бюджет неопределенности и получают оценку суммарной стандартной неопределенности. Каждый из этапов измерения рассматривают по отдельности. Неопределенность измерения, возникающую на каждом из этапов, оценивают независимо, экспериментальным или другими методами.
Для оценивания неопределенности, связанной с отбором пробы, часто используют теоретическую модель Ги. На рисунке 2 показана классификация погрешностей отбора пробы, предложенная Ги. Общая погрешность определения ("глобальной погрешностью оценки" (GEE)), состоит из суммарной погрешности отбора пробы (TSE) и суммарной погрешности анализа (TAE):
GEE = TSE + TAE
TSE = (PSE + FSE + GSE) + (IDE + IXE + IPE) + SWE
Составляющие TSE можно разделить на две основные группы:
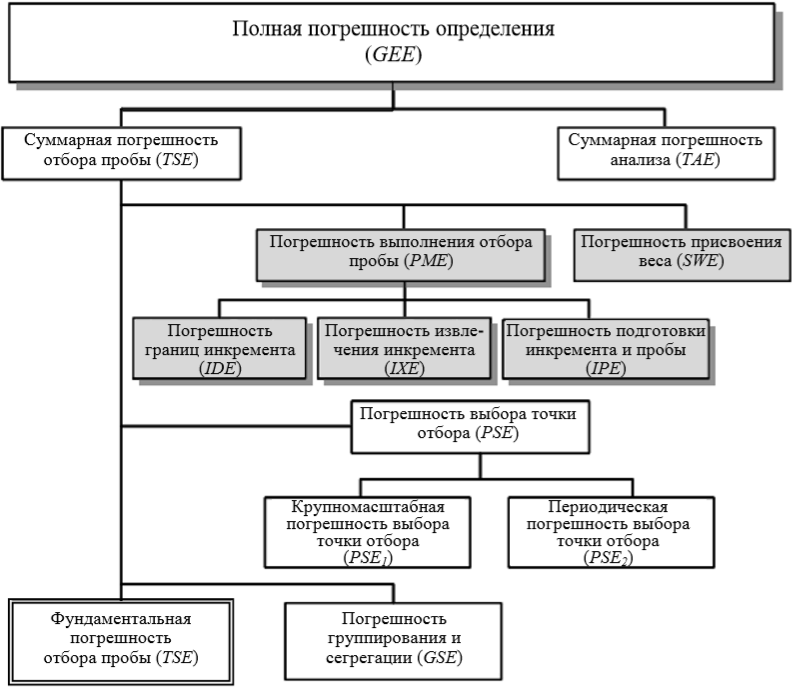
* погрешности некорректного отбора пробы показаны затененными прямоугольниками, и их не включают в оценку неопределенности
Рисунок 2. Классификация погрешностей отбора пробы по теории отбора проб Ги
Некоторые погрешности от некорректного отбора пробы можно отнести к грубым промахам, и их не следует включать в оценку неопределенности. Погрешности в рамках корректного отбора пробы не связаны с какими-либо нарушениями процедуры, и их можно рассматривать как возможные источники неопределенности.
Принципиальное преимущество теоретического подхода состоит в том, что он позволяет детально оценить известные источники неопределенности и легко выявить самый существенный. Этот подход уместно применять для хорошо изученных аналитических задач, которые предполагается решать в течение длительного времени.
К недостаткам теоретического подхода относят то, что для расчета неопределенности могут понадобиться предварительные детальные исследования параметров пробы и характера их изменения в пределах целевого объекта. Следовательно, приходится делать идеализированные допущения о составе материала. Этот подход с применением теории отбора пробы требует оценок или допущений относительно восьми типов погрешности отбора пробы, а также того, как они могут меняться в пределах целевого объекта.
Помимо получения первичной единичной оценки неопределенности для конкретной схемы отбора проб, примененной к конкретному целевому объекту, регулярное применение "метода двойных проб" может быть также полезно как способ постоянного контроля качества отбора пробы. Таким образом можно учесть то, как влияет на неопределенность изменение неоднородности целевого объекта от одного случая отбора пробы до другого при использовании одной и той же методики отбора. При этом мы получаем количественное подтверждение качества отбора проб, а не просто полагаемся на допущение о том, что пробы будет репрезентативными, если их отбирать по правильной схеме.
Для успешного применения оценки неопределенности имеет смысл:
Валидация для конкретного применения включает в себя однократную оценку составляющих неопределенности в условиях, ожидаемых при рутинном применении процедуры пробоотбора, демонстрирует, какие величины неопределенности измерений могут быть получены, и согласуется ли это с требованиями к измерению.
Контроль качества результатов измерений необходим для демонстрации постоянства составляющих неопределенности, установленных при валидации.
Такой контроль проводят путем взятия двух проб из каждого объекта пробоотбора и полного дублирования плана пробоотбора. Каждую пробу анализируют и вычисляют разницу между двумя результатами измерений по формуле:
D = | х1 - х2 | ,
где х1 и х2 — результаты измерений, полученные для первой и второй проб.
Затем рассчитывают суммарную стандартную неопределенность по формуле:
u = (u2sample + u2analysis)0,5 ,
где usample и uanalysis — неопределенности пробоотбора и анализа соответственно, установленные при процедуре оценки пригодности плана пробоотбора.
В соответствии с ГОСТ Р ИСО 5725-6 строят контрольную карту Шухарта (R-карту) с пределом предупреждения 2,83u и пределом действия 3,69u при числе наблюдений 2. Значение D, превышающее предел предупреждения или предел действия, свидетельствует о том, что результат должен быть тщательно проверен. Такой результат может являться результатом нарушения и при пробоотборе, и при анализе.
Существуют разные источники погрешности и неопределенности в процессе отбора проб. Согласно IUPAC неоднородность объекта пробоотбора и ее последствия, такие как случайный разброс и смещение, связанное с отбором, остаются самой большой проблемой для правильной организации отбора проб и, в целом, самым существенным источником неопределенности отбора проб.
1. Руководство по методам и подходам Eurachem / CITAC. Неопределенность измерения, связанная с отбором пробы. Первое издание 2007.
2. ГОСТ Р 8.878-2014 Государственная система обеспечения единства измерений (ГСИ). Учет и контроль ядерных
материалов. Система измерений. Оценивание неопределенности пробоотбора.
3. ГОСТ Р ИСО 5725-3-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода
измерений.
4. ГОСТ ISO/IEC 17025-2019 Общие требования к компетентности испытательных и калибровочных лабораторий.
20 мая 2020 г. 14:29
 Записаться
Записаться
 Записаться
Записаться
 Записаться
Записаться
.jpg) Записаться
Записаться
.png) Записаться
Записаться